|
| |
 |
Special Projects
- The transit of the
Planet Mercury
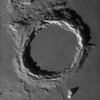
On May 9, 2016 a rare transit of Mercury in front oft
the Sun took place. At time of the transit Mercury's distance to Earth was
about 83,371,000 kilometers and it was seen as a small disk with a diameter of
12.1 arcseconds.
« The left image (11:14:09 UTC) shows Mercury
at the ingress.
Back to Special
Projects |
|
 |
|
|
May
9, 2016 - A transit of Mercury and the attempt on simultaneous observations
from Namibia and Germany to derive the parallax of Mercury and thus the
distance from the Sun and the value of the astronomical
unit.
In principle, a Mercury
or Venus transit in front of the solar disk (albeit very rarely) is rather a
boring affair, although the observers can practically see the dynamics of the
solar system. The animation on the right shows 5 stages of the beginning
transit from 11:14 to 11:19 UTC, taken in Namibia (orientation: east left,
south top). The used telescope was a 75mm Pentax refractor with 500 mm focal
length, fitted with a 60mm Coronado H-alpha filter with a half-width of about
0.7 angstroms. The camera was a Celestron video module SkyRis 445 mono
(stacking of 12% out of 1200 frames).
» The image at right
beautifully shows the solar chromosphere. Compared to Mercury (nearly 4880 km
diameter = 7.12 arcsec) you can clearly see how thin the chromosphere is in relation to the solar diameter. Also clearly visible that Mercury has missed
the covering of a small protuberance at the ingress by some
arcseconds
 |
To capture not only the usual photo series of transit, we had thought
about whether it is possible to measure the parallax of Mercury and then to
compute
the solar distance and the fundamental value of the astronomical unit with
amateur equipment and image processing tools.
Therefore we agreed with a
friend, Dirk Lucius in Ostfriesland, to take avifiles every 15 minutes at the
same time with similar equipment.
« The left picture shows the parallax of
Mercury, based on the solar chromosphere, at exactly 14:00:15 UTC (midtime of
the Avifiles) between Leer / Ostfriesland and Onjala Lodge in Namibia. The
focal lengths were about 1.000 millimeters. The displacement is approximately
3/4 of the apparent Mercury diameter.
All of the following images can be enlarged by
clicking on it. |
|
 |
|
|
|
The
Station Onjala (22 ° 12 ' 24.2'' south, 17 ° 34 ' 58.8 " east,
height about 1724 m above sea level)
To get optimal seeing conditions we
put the telescope on the transportable mount and not in the dome. The 75mm
Pentax refractor with 500mm focal length was set up parallel to a fixed mounted
C11 with HyperStar so that the objective of the C11 pointed to the ground and
the main mirror cell of the C11 was covered with rescue foil to minimize
thermal gradients.
A Celestron video module Skyris 445 M with a pixel
size of 3.75microns was used for capturing the avifiles. Each avifile had a
length of |
 |
 |
|
700 frames,
of which 20% have been stacked. The computer clock was set with an accuracy of
below 1 second with the help of a GPS handheld receiver. It can be clearly seen
in the above images that the weather conditions in Namibia were far from
optimal. We had during our whole stay on Onjala nearly every day the same
situation: in the morning was a clear blue sky and from noon rising convective clouds
and in the evening a mostly complete covered sky.
Due to the increasing
clouds we could significantly take less Avifiles than we had planned. Overall,
we had finally only six simultaneous recordings for a further
analysis.
For measureing the parallax of Mercury we needed as many
details and fine structures on the solar disk as possible. So we took H-alpha
images of the solar chromosphere. On Onjala a 60mm Coronado (HWB approximately
0.7 Ångström) and in Ostfriesland a 2-fold stacked 90mm Coronado
filter (HWB about 0.5 Angstroms) was used.
|
 |
 |
While
for one of us (Paech) a 4 hours sweating session under a towel (shading of the
laptop screen) started, the other one of us (Hofmann) was in the 4m dome and
took images at the Zeiss APQ refractor (150 / 1200mm) with a Canon 6D and an
old Baader Herschel prism images in white light.
In the following are
some white light, H-alpha images and animations of the Mercury transit. Because
of the rapidly increasing cloudiness we stopped taking images at 15:30 UTC
(17:30 CEST). In Namibia the sun was setting around 16:30 UTC. |
|
|
|
Above 4 white light images taken with the Zeiss APQ refractor, Canon 6D and
an old Baader Herschel prism (image orientation: east left, north up). The two
images on the left were taken shortly after the ingress. The picture on the
right just before stopping our image session due to the dense cloud coverage.
The images can be enlarged by clicking.
|
 |
To
the H-alpha images of Onjala. (Click to load a large images): The left
image shows the entire sun at 12:45 UTC with the three marked active regions
NOAA 2541, 2542 and 2543.
Further images taken at different phases of
transit showing the entire sun: 11:02 (still without Mercury), 11:31, 12:15,
13:17 and 14:51
11:02
(still without Mercury),
11:31,
12:15,
13:17
und 14:51 (all times are UTC). (all times are UTC). Below we
show two animations which can be enlarged by clicking on them. left: 14:11 to
14:33 UTC, captured with f = 1.000 mm and right 11:15 to 13:50 UTC with f = 500
mm.
 |
 |
Note the changing chromospheric phenomena. |
|
|
The station Leer in Ostfriesland
(N 53 ° 14 '44.4 ", E 07 ° 28' 36.0", height about 3 m above sea
level)
In Germany Dirk Lucius watched the transit of Mercury at the same
time. He used a 90mm refractor with a Coronado Double Stack H-alpha filter. The
camera was the same as in Namibia - a Celestron video module SkyRis 445 M. The
focal length oft he telescope has been extended with a Baader FFC module to
about 1.000 mm.
The image far
right shows the average quality of the summed video images of Dirk. Both images
can be enlarged by clicking. |
 |
 |
|
In addition
to the simultaneous images fort he parallax measurement Dirk was still working
with its 150 mm refractor and exposed images in the three spectral ranges (from
left to right) continuum (white light), the calcium and in H-alpha light with
different focal lengths.
|
|
Measurement of the parallax of Mercury and
the determination of the astronomical unit
(AU)
|
 |
Knowing on one hand the parallax of a celestial body with respect to
much more distant background objects and on the other hand the distance between
the two observation stations \(\Delta P\) The distance of the celestial body
can be purely geometrically determined from these two measured values. In most
cases the parallax angle \(\pi\) are very small angles in astronomy. This
simplifies the calculation and the distance \(d\) to the body S. S can be
determined using the simple formula, see
figure 1
on the left: $$d = \frac{\Delta P}{\pi}$$ |
|
Unfortunately, the parallax of the Sun and thus the AU can not be
measured directly in the context of a quasi "infinitely" distant star. However,
the observation of a transit of Mercury or Venus and the knowledge of the
relative distances in the solar system, for example, based on the Kepler's
third law, gives an access to the Astronomical Unit.
|
| The
approach we use is based on the simultaneous observation of the position of
Mercury in front of the Sun. The recorded images from Leer and Onjala were
matched together and the remaining parallax of Mercury \(\pi'_M\) determined
with respect to the solar surface. \(\pi'_M\) is a combination of the parallax
of the sun \(\pi_S\) and Mercury \(\pi_M\) relative to the background stars, as
shown in Figure 2 (right). In the left part, the Sun, Mercury's disc and the
background stars are shown as they appear from the location 1 on the Earth. In
the central part of the picture, the view of the Sun and Mercury from location
2 on the Earth is superimposed. Relative to the fixed background stars the
parallax of Mercury and the Sun could be read here. But the background stars
but not visible during daylight, only the parallax with respect to the Sun's
surface can be determined (right part) with\(\pi'_M=\pi_M-\pi_S\). |
 |
|
From
long-term observations the relative distances between Earth and Mercury
\(d_{M}\) and Earth and Sun \(d_S\) at the transit time can be determined in
multiples of AE. Since these observations are beyond our possibilities, we used
the site www.calsky.com
to determine these quantities. We found the factors
\(d_S=1.01\) and \(d_M=0.558\).
The astronomical unit is designated in
the following formula with x and can be computed with the quantities from above
to $$x=\frac{\Delta P}{\pi'_Md_S}\left(\frac{d_s}{d_M}-1\right)$$. The
derivation is described in detail in our
formulary (in German)
.
The determination of Mercury's parallax
\(\pi'_M\) in corresponding images will be briefly described
below.
|
- Determination of the scale
of the Onjala images with the help of the Sun's diameter of 1900.8 arcseconds
(www.calsky.com) for the
transit period.
- Matching of the images from
Leer to the Onjala images based on the H-α structures. To reduce the
effort for a manual referencing in Photoshop, the recordings were skaled by
factor of 8 (Onjala) and 4 (Leer), 2 artificial stars were copied at prominent
H-α structures
(see
Figure 3 on the right) and automatically aligned in the program MaximDL.
- Determination of the pixel
coordinates of Mercury's discs in the two images for each observation time.
This was done in the scaled images by creating a large circle around Mercury in
Photoshop and using the function "free transformation" until the disc of Mercury
was centered. The displayed pixel coordinates of the center will be used as the
measured position values,
see Figure
4.
- Conversion of the distance
in pixels into the parallax \(\pi'_M\) in the sky with help of the imaging
scale and the scaling factor of the Onjala images.
|

Figure
3 |
|
- With the help of the station
coordinates (length, width, height) of Leer and Onjala the position vectors
\(\vec{p}_2\) and \(\vec{p}_1\) are calculated in an Earth-fixed cartesian
reference system.
- Rotation of the two vectors in the
ICRS (see below) with rotation data from the
Earth Orientation Center.
- Determination of the vector
\(\vec{g}_0\), that is the direction to Mercury in space, with data of JPL
Horizons website. In principle this vector can be determined with knowledge of
the position of Mercury in the sky and the time, but here we save us this
work.
The reduced distance is
calculated with the cross product of the vectors $$\Delta
P=\left|\left(\vec{p}_2-\vec{p}_1\right)\times\vec{g}_0\right|.$$ |
 |
| Figure
4 » |
|
| |
 |
The
calculation of the reduced distance \(\Delta P\), perpendicular to the
direction from the observation location to Mercury, between Onjala and Leer is
briefly summarized here. The necessary steps and formulas are listed in the
formulary. The basis,
considered separately for each observation time, are spatial triangles between
Merkur - Onjala (\(P_2\)) - Leer (\(P_1\)).
Figure
5 (left) shows an example triangle and the vectors used therein. For the
calculation it is important that all vectors are present in a common coordinate
system. Here the independently of the Earth's rotation celestial reference
system ICRS is useful. |
| « Figure
5 |
|
| |
The table
lists the results of the parallax of Mercury \(\pi'_M\), related to the solar
surface, the reduced distance \(\Delta P\) between Onjala and Leer and the
calculated values for the astronomical unit \(x\) for each measurement time.
The mean value is 149,931,751 km with a standard deviation of 5.6 million km
|
| Measuring time [UTC] |
\(\pi'_M\) ["] |
\(\Delta P\) [km] |
\(x\) [km] |
| |
|
|
|
| 11:15:12.5 |
8.516 |
7807.17 |
151 657 264 |
| 12:30:12.5 |
8.936 |
7782.32 |
144 068 962 |
| 13:00:12.5 |
8.263 |
7761.36 |
155 383 158 |
| 13:15:12.5 |
9.044 |
7747.67 |
141 722 132 |
| 13:45:12.5 |
8.263 |
7712.88 |
154 413 326 |
| 14:00:12.5 |
8.352 |
7691.46 |
152 345 665 |
The animation on
the right shows the parallaxe with respect to the solar chromosphere between
Leer and Onjala at 14:00:00 UTC » |
 |
|
At the beginning of this project we had not believed that it is
possible to determine the astronomical unit so accurately with the used small
instruments. The difference to the SI value of the astronomical unit is on
average just 334,000 km, i.e. slightly less than the average distance between
Earth and Moon.
|
|
|
| All Images and all Content on this page are © by
Franz Hofmann, Wolfgang Paech und Dirk Lucius |